mlpack
K-Means tutorial (kmeans)

Introduction

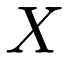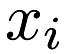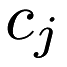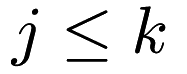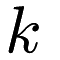The popular k-means algorithm for clustering has been around since the late 1950s, and the standard algorithm was proposed by Stuart Lloyd in 1957. Given a set of points $ X $, k-means clustering aims to partition each point $ x_i $ into a cluster $ c_j $ (where $ j \le k $ and $ k $, the number of clusters, is a parameter). The partitioning is done to minimize the objective function

\[ \sum_{j = 1}^{k} \sum_{x_i \in c_j} \| x_i - \mu_j \|^2 \]

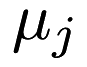where $\mu_j$ is the centroid of cluster 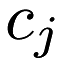$c_j$. The standard algorithm is a two-step algorithm:

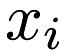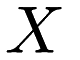  • Assignment step. Each point $x_i$ in $X$ is assigned to the cluster whose centroid it is closest to.
  • Update step. Using the new cluster assignments, the centroids of each cluster are recalculated.

The algorithm has converged when no more assignment changes are happening with each iteration. However, this algorithm can get stuck in local minima of the objective function and is particularly sensitive to the initial cluster assignments. Also, situations can arise where the algorithm will never converge but reaches steady state – for instance, one point may be changing between two cluster assignments.

There is vast literature on the k-means algorithm and its uses, as well as strategies for choosing initial points effectively and keeping the algorithm from converging in local minima. mlpack does implement some of these, notably the Bradley-Fayyad algorithm (see the reference below) for choosing refined initial points. Importantly, the C++ KMeans class makes it very easy to improve the k-means algorithm in a modular way.

@inproceedings{bradley1998refining,
title={Refining initial points for k-means clustering},
author={Bradley, Paul S. and Fayyad, Usama M.},
booktitle={Proceedings of the Fifteenth International Conference on Machine
Learning (ICML 1998)},
volume={66},
year={1998}
}

mlpack provides:

Table of Contents

A list of all the sections this tutorial contains.

Command-Line 'kmeans'

mlpack provides a command-line executable, mlpack_kmeans, to allow easy execution of the k-means algorithm on data. Complete documentation of the executable can be found by typing

$ mlpack_kmeans --help

As of October 2014, support for overclustering has been removed due to bugs and lack of usage. If this is support you were using, or are interested, please file a bug or get in touch with the mlpack developers in some way so that the support can be re-implemented.

Below are several examples demonstrating simple use of the mlpack_kmeans executable.

Simple k-means clustering

We want to find 5 clusters using the points in the file dataset.csv. By default, if any of the clusters end up empty, that cluster will be reinitialized to contain the point furthest from the cluster with maximum variance. The cluster assignments of each point will be stored in assignments.csv. Each row in assignments.csv will correspond to the row in dataset.csv.

$ mlpack_kmeans -c 5 -i dataset.csv -v -o assignments.csv

Saving the resulting centroids

Sometimes it is useful to save the centroids of the clusters found by k-means; one example might be for plotting the points. The -C (–centroid_file) option allows specification of a file into which the centroids will be saved (one centroid per line, if it is a CSV or other text format).

$ mlpack_kmeans -c 5 -i dataset.csv -v -o assignments.csv -C centroids.csv

Allowing empty clusters

If you would like to allow empty clusters to exist, instead of reinitializing them, simply specify the -e (–allow_empty_clusters) option. Note that when you save your clusters, even empty clusters will still have centroids. The centroids of the empty cluster will be the same as what they were on the last iteration when the cluster was not empty.

$ mlpack_kmeans -c 5 -i dataset.csv -v -e -o assignments.csv -C centroids.csv

Killing empty clusters

If you would like to kill empty clusters , instead of reinitializing them, simply specify the -E (–kill_empty_clusters) option. Note that when you save your clusters, all the empty clusters will be removed and the final result may contain less than specified number of clusters.

$ mlpack_kmeans -c 5 -i dataset.csv -v -E -o assignments.csv -C centroids.csv

Limiting the maximum number of iterations

As mentioned earlier, the k-means algorithm can often fail to converge. In such a situation, it may be useful to stop the algorithm by way of limiting the maximum number of iterations. This can be done with the -m (–max_iterations) parameter, which is set to 1000 by default. If the maximum number of iterations is 0, the algorithm will run until convergence – or potentially forever. The example below sets a maximum of 250 iterations.

$ mlpack_kmeans -c 5 -i dataset.csv -v -o assignments.csv -m 250

Using Bradley-Fayyad "refined start"

The method proposed by Bradley and Fayyad in their paper "Refining initial points for k-means clustering" is implemented in mlpack. This strategy samples points from the dataset and runs k-means clustering on those points multiple times, saving the resulting clusters. Then, k-means clustering is run on those clusters, yielding the original number of clusters. The centroids of those resulting clusters are used as initial centroids for k-means clustering on the entire dataset.

This technique generally gives better initial points than the default random partitioning, but depending on the parameters, it can take much longer. This initialization technique is enabled with the -r (–refined_start) option. The -S (–samplings) parameter controls how many samplings of the dataset are performed, and the -p (–percentage) parameter controls how much of the dataset is randomly sampled for each sampling (it must be between 0.0 and 1.0). For more information on the refined start technique, see the paper referenced in the introduction of this tutorial.

The example below performs k-means clustering, giving 5 clusters, using the refined start technique, sampling 10% of the dataset 25 times to produce the initial centroids.

$ mlpack_kmeans -c 5 -i dataset.csv -v -o assignments.csv -r -S 25 -p 0.2

Using different k-means algorithms

The mlpack_kmeans program implements six different strategies for clustering; each of these gives the exact same results, but will have different runtimes. The particular algorithm to use can be specified with the -a or –algorithm option. The choices are:

  • naive: the standard Lloyd iteration; takes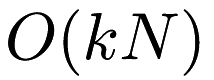 $O(kN)$ time per iteration.
  • pelleg-moore: the 'blacklist' algorithm, which builds a kd-tree on the data. This can be fast when k is small and the dimensionality is reasonably low.
  • elkan: Elkan's algorithm for k-means, which maintains upper and lower distance bounds between each point and each centroid. This can be very fast, but it does not scale well to the case of large N or k, and uses a lot of memory.
  • hamerly: Hamerly's algorithm is a variant of Elkan's algorithm that handles memory usage much better and thus can operate with much larger datasets than Elkan's algorithm.
  • dualtree: The dual-tree algorithm for k-means builds a kd-tree on both the centroids and the points in order to prune away as much work as possible. This algorithm is most effective when both N and k are large.
  • dualtree-covertree: This is the dual-tree algorithm using cover trees instead of kd-trees. It satisfies the runtime guarantees specified in the dual-tree k-means paper.

In general, the naive algorithm will be much slower than the others on datasets that are larger than tiny.

The example below uses the dualtree algorithm to perform k-means clustering with 5 clusters on the dataset in dataset.csv, using the initial centroids in initial_centroids.csv, saving the resulting cluster assignments to assignments.csv:

$ mlpack_kmeans -i dataset.csv -c 5 -v -I initial_centroids.csv -a dualtree \
> -o assignments.csv

The 'KMeans' class

The KMeans<> class (with default template parameters) provides a simple way to run k-means clustering using mlpack in C++. The default template parameters for KMeans<> will initialize cluster assignments randomly and disallow empty clusters. When an empty cluster is encountered, the point furthest from the cluster with maximum variance is set to the centroid of the empty cluster.

Running k-means and getting cluster assignments

The simplest way to use the KMeans<> class is to pass in a dataset and a number of clusters, and receive the cluster assignments in return. Note that the dataset must be column-major – that is, one column corresponds to one point. See the matrices guide for more information.

#include <mlpack/methods/kmeans/kmeans.hpp>
using namespace mlpack::kmeans;
// The dataset we are clustering.
extern arma::mat data;
// The number of clusters we are getting.
extern size_t clusters;
// The assignments will be stored in this vector.
arma::Row<size_t> assignments;
// Initialize with the default arguments.
KMeans<> k;
k.Cluster(data, clusters, assignments);

Now, the vector assignments holds the cluster assignments of each point in the dataset.

Running k-means and getting centroids of clusters

Often it is useful to not only have the cluster assignments, but the centroids of each cluster. Another overload of Cluster() makes this easily possible:

#include <mlpack/methods/kmeans/kmeans.hpp>
using namespace mlpack::kmeans;
// The dataset we are clustering.
extern arma::mat data;
// The number of clusters we are getting.
extern size_t clusters;
// The assignments will be stored in this vector.
arma::Row<size_t> assignments;
// The centroids will be stored in this matrix.
arma::mat centroids;
// Initialize with the default arguments.
KMeans<> k;
k.Cluster(data, clusters, assignments, centroids);

Note that the centroids matrix has columns equal to the number of clusters and rows equal to the dimensionality of the dataset. Each column represents the centroid of the according cluster – centroids.col(0) represents the centroid of the first cluster.

Limiting the maximum number of iterations

The first argument to the constructor allows specification of the maximum number of iterations. This is useful because often, the k-means algorithm does not converge, and is terminated after a number of iterations. Setting this parameter to 0 indicates that the algorithm will run until convergence – note that in some cases, convergence may never happen. The default maximum number of iterations is 1000.

// The first argument is the maximum number of iterations. Here we set it to
// 500 iterations.
KMeans<> k(500);

Then you can run Cluster() as normal.

Setting initial cluster assignments

If you have an initial guess for the cluster assignments for each point, you can fill the assignments vector with the guess and then pass an extra boolean (initialAssignmentGuess) as true to the Cluster() method. Below are examples for either overload of Cluster().

#include <mlpack/methods/kmeans/kmeans.hpp>
using namespace mlpack::kmeans;
// The dataset we are clustering on.
extern arma::mat dataset;
// The number of clusters we are obtaining.
extern size_t clusters;
// A vector pre-filled with initial assignment guesses.
extern arma::Row<size_t> assignments;
KMeans<> k;
// The boolean set to true indicates that our assignments vector is filled with
// initial guesses.
k.Cluster(dataset, clusters, assignments, true);
#include <mlpack/methods/kmeans/kmeans.hpp>
using namespace mlpack::kmeans;
// The dataset we are clustering on.
extern arma::mat dataset;
// The number of clusters we are obtaining.
extern size_t clusters;
// A vector pre-filled with initial assignment guesses.
extern arma::Row<size_t> assignments;
// This will hold the centroids of the finished clusters.
arma::mat centroids;
KMeans<> k;
// The boolean set to true indicates that our assignments vector is filled with
// initial guesses.
k.Cluster(dataset, clusters, assignments, centroids, true);
Note
If you have a heuristic or algorithm which makes initial guesses, a more elegant solution is to create a new class fulfilling the InitialPartitionPolicy template policy. See the section about changing the initial partitioning strategy for more details.
Note
If you set the InitialPartitionPolicy parameter to something other than the default but give an initial cluster assignment guess, the InitialPartitionPolicy will not be used to initialize the algorithm. See the section about changing the initial partitioning strategy for more details.

Setting initial cluster centroids

An equally important option to being able to make initial cluster assignment guesses is to make initial cluster centroid guesses without having to assign each point in the dataset to an initial cluster. This is similar to the previous section, but now you must pass two extra booleans – the first (initialAssignmentGuess) as false, indicating that there are not initial cluster assignment guesses, and the second (initialCentroidGuess) as true, indicating that the centroids matrix is filled with initial centroid guesses.

This, of course, only works with the overload of Cluster() that takes a matrix to put the resulting centroids in. Below is an example.

#include <mlpack/methods/kmeans/kmeans.hpp>
using namespace mlpack::kmeans;
// The dataset we are clustering on.
extern arma::mat dataset;
// The number of clusters we are obtaining.
extern size_t clusters;
// A matrix pre-filled with guesses for the initial cluster centroids.
extern arma::mat centroids;
// This will be filled with the final cluster assignments for each point.
arma::Row<size_t> assignments;
KMeans<> k;
// Remember, the first boolean indicates that we are not giving initial
// assignment guesses, and the second boolean indicates that we are giving
// initial centroid guesses.
k.Cluster(dataset, clusters, assignments, centroids, false, true);
Note
If you have a heuristic or algorithm which makes initial guesses, a more elegant solution is to create a new class fulfilling the InitialPartitionPolicy template policy. See the section about changing the initial partitioning strategy for more details.
Note
If you set the InitialPartitionPolicy parameter to something other than the default but give an initial cluster centroid guess, the InitialPartitionPolicy will not be used to initialize the algorithm. See the section about changing the initial partitioning strategy for more details.

Running sparse k-means

The Cluster() function can work on both sparse and dense matrices, so all of the above examples can be used with sparse matrices instead, if the fifth template parameter is modified. Below is a simple example. Note that the centroids are returned as a dense matrix, because the centroids of collections of sparse points are not generally sparse.

// The sparse dataset.
extern arma::sp_mat sparseDataset;
// The number of clusters.
extern size_t clusters;
// The assignments will be stored in this vector.
arma::Row<size_t> assignments;
// The centroids of each cluster will be stored in this sparse matrix.
arma::sp_mat sparseCentroids;
// We must change the fifth (and last) template parameter.
KMeans<metric::EuclideanDistance, SampleInitialization, MaxVarianceNewCluster,
NaiveKMeans, arma::sp_mat> k;
k.Cluster(sparseDataset, clusters, assignments, sparseCentroids);

Template parameters for the 'KMeans' class

The KMeans<> class also takes three template parameters, which can be modified to change the behavior of the k-means algorithm. There are three template parameters:

  • MetricType: controls the distance metric used for clustering (by default, the squared Euclidean distance is used)
  • InitialPartitionPolicy: the method by which initial clusters are set; by default, SampleInitialization is used
  • EmptyClusterPolicy: the action taken when an empty cluster is encountered; by default, MaxVarianceNewCluster is used
  • LloydStepType: this defines the strategy used to make a single Lloyd iteration; by default this is the typical Lloyd iteration specified in NaiveKMeans
  • MatType: type of data matrix to use for clustering

The class is defined like below:

template<
typename DistanceMetric = mlpack::metric::SquaredEuclideanDistance,
typename InitialPartitionPolicy = SampleInitialization,
typename EmptyClusterPolicy = MaxVarianceNewCluster,
template<class, class> class LloydStepType = NaiveKMeans,
typename MatType = arma::mat
>
class KMeans;

In the following sections, each policy is described further, with examples of how to modify them.

Changing the distance metric used for k-means

Most machine learning algorithms in mlpack support modifying the distance metric, and KMeans<> is no exception. Similar to NeighborSearch (see the section in the NeighborSearch tutorial), any class in mlpack::metric can be given as an argument. The mlpack::metric::LMetric class is a good example implementation.

A class fulfilling the MetricType policy must provide the following two functions:

// Empty constructor is required.
MetricType();
// Computer the distance between two points.
template<typename VecType>
double Evaluate(const VecType& a, const VecType& b);

Most of the standard metrics that could be used are stateless and therefore the Evaluate() method is implemented statically. However, there are metrics, such as the Mahalanobis distance (mlpack::metric::MahalanobisDistance), that store state. To this end, an instantiated MetricType object is stored within the KMeans class. The example below shows how to pass an instantiated MahalanobisDistance in the constructor.

// The initialized Mahalanobis distance.
extern mlpack::metric::MahalanobisDistance distance;
// We keep the default arguments for the maximum number of iterations, but pass
// our instantiated metric.
KMeans<mlpack::metric::MahalanobisDistance> k(1000, distance);
Note
While the MetricType policy only requires two methods, one of which is an empty constructor, more can always be added. mlpack::metric::MahalanobisDistance also has constructors with parameters, because it is a stateful metric.

Changing the initial partitioning strategy used for k-means

There have been many initial cluster strategies for k-means proposed in the literature. Fortunately, the KMeans<> class makes it very easy to implement one of these methods and plug it in without needing to modify the existing algorithm code at all.

By default, the KMeans<> class uses mlpack::kmeans::SampleInitialization, which randomly samples points as initial centroids. However, writing a new policy is simple; it needs to only implement the following functions:

// Empty constructor is required.
InitialPartitionPolicy();
// Only *one* of the following two functions is required! You should implement
// whichever you find more convenient to implement.
// This function is called to initialize the clusters and returns centroids.
template<typename MatType>
void Cluster(MatType& data,
const size_t clusters,
arma::mat& centroids);
// This function is called to initialize the clusters and returns individual
// point assignments. The centroids will then be calculated from the given
// assignments.
template<typename MatType>
void Cluster(MatType& data,
const size_t clusters,
arma::Row<size_t> assignments);

The templatization of the Cluster() function allows both dense and sparse matrices to be passed in. If the desired policy does not work with sparse (or dense) matrices, then the method can be written specifically for one type of matrix – however, be warned that if you try to use KMeans with that policy and the wrong type of matrix, you will get many ugly compilation errors!

// The Cluster() function specialized for dense matrices.
void Cluster(arma::mat& data,
const size_t clusters,
arma::Row<size_t> assignments);

Note that only one of the two possible Cluster() functions are required. This is because sometimes it is easier to express an initial partitioning policy as something that returns point assignments, and sometimes it is easier to express the policy as something that returns centroids. The KMeans<> class will use whichever of these two functions is given; if both are given, the overload that returns centroids will be preferred.

One alternate to the default SampleInitialization policy is the RefinedStart policy, which is an implementation of the Bradley and Fayyad approach for finding initial points detailed in "Refined initial points for k-means clustering" and other places in this document. Another option is the RandomPartition class, which randomly assigns points to clusters, but this may not work very well for most settings. See the documentation for mlpack::kmeans::RefinedStart and mlpack::kmeans::RandomPartition for more information.

If the Cluster() method returns point assignments instead of centroids, then valid initial assignments must be returned for every point in the dataset.

As with the MetricType template parameter, an initialized InitialPartitionPolicy can be passed to the constructor of KMeans as a fourth argument.

Changing the action taken when an empty cluster is encountered

Sometimes, during clustering, a situation will arise where a cluster has no points in it. The KMeans class allows easy customization of the action to be taken when this occurs. By default, the point furthest from the centroid of the cluster with maximum variance is taken as the centroid of the empty cluster; this is implemented in the mlpack::kmeans::MaxVarianceNewCluster class. Another alternate choice is the mlpack::kmeans::AllowEmptyClusters class, which simply allows empty clusters to persist.

A custom policy can be written and it must implement the following methods:

// Empty constructor is required.
EmptyClusterPolicy();
// This function is called when an empty cluster is encountered. emptyCluster
// indicates the cluster which is empty, and then the clusterCounts and
// assignments are meant to be modified by the function. The function should
// return the number of modified points.
template<typename MatType>
size_t EmptyCluster(const MatType& data,
const size_t emptyCluster,
const MatType& centroids,
arma::Col<size_t>& clusterCounts,
arma::Row<size_t>& assignments);

The EmptyCluster() function is called for each cluster that is empty at each iteration of the algorithm. As with InitialPartitionPolicy, the EmptyCluster() function does not need to be generalized to support both dense and sparse matrices – but usage with the wrong type of matrix will cause compilation errors.

Like the other template parameters to KMeans, EmptyClusterPolicy implementations that have state can be passed to the constructor of KMeans as a fifth argument. See the kmeans::KMeans documentation for further details.

The LloydStepType template parameter

The internal algorithm used for a single step of the k-means algorithm can easily be changed; mlpack implements several existing classes that satisfy the LloydStepType policy:

Note that the LloydStepType policy is itself a template template parameter, and must accept two template parameters of its own:

  • MetricType: the type of metric to use
  • MatType: the type of data matrix to use

The LloydStepType policy also mandates three functions:

  • a constructor: LloydStepType(const MatType& dataset, MetricType& metric);
  • an Iterate() function:
double Iterate(const arma::mat& centroids,
arma::mat& newCentroids,
arma::Col<size_t>& counts);
  • a function to get the number of distance calculations:
size_t DistanceCalculations() const { return distanceCalculations; }

Note that Iterate() does not need to return valid centroids if the cluster is empty. This is because EmptyClusterPolicy will handle the empty centroid. This behavior can be used to avoid small amounts of computation.

For examples, see the five aforementioned implementations of classes that satisfy the LloydStepType policy.

Further documentation

For further documentation on the KMeans class, consult the complete API documentation.