An implementation of LARS, a stage-wise homotopy-based algorithm for l1-regularized linear regression (LASSO) and l1+l2 regularized linear regression (Elastic Net). More...

Public Member Functions
	LARS (const bool useCholesky=false, const double lambda1=0.0, const double lambda2=0.0, const double tolerance=1e-16)
	Set the parameters to LARS. More...

	LARS (const bool useCholesky, const arma::mat &gramMatrix, const double lambda1=0.0, const double lambda2=0.0, const double tolerance=1e-16)
	Set the parameters to LARS, and pass in a precalculated Gram matrix. More...

	LARS (const arma::mat &data, const arma::rowvec &responses, const bool transposeData=true, const bool useCholesky=false, const double lambda1=0.0, const double lambda2=0.0, const double tolerance=1e-16)
	Set the parameters to LARS and run training. More...

	LARS (const arma::mat &data, const arma::rowvec &responses, const bool transposeData, const bool useCholesky, const arma::mat &gramMatrix, const double lambda1=0.0, const double lambda2=0.0, const double tolerance=1e-16)
	Set the parameters to LARS, pass in a precalculated Gram matrix, and run training. More...

	LARS (const LARS &other)
	Construct the LARS object by copying the given LARS object. More...

	LARS (LARS &&other)
	Construct the LARS object by taking ownership of the given LARS object. More...

const std::vector< size_t > &	ActiveSet () const
	Access the set of active dimensions. More...

const arma::vec &	Beta () const
	Access the solution coefficients. More...

const std::vector< arma::vec > &	BetaPath () const
	Access the set of coefficients after each iteration; the solution is the last element. More...

double	ComputeError (const arma::mat &matX, const arma::rowvec &y, const bool rowMajor=false)
	Compute cost error of the given data matrix using the currently-trained LARS model. More...

double	Lambda1 () const
	Get the L1 regularization coefficient. More...

double &	Lambda1 ()
	Modify the L1 regularization coefficient. More...

double	Lambda2 () const
	Get the L2 regularization coefficient. More...

double &	Lambda2 ()
	Modify the L2 regularization coefficient. More...

const std::vector< double > &	LambdaPath () const
	Access the set of values for lambda1 after each iteration; the solution is the last element. More...

const arma::mat &	MatUtriCholFactor () const
	Access the upper triangular cholesky factor. More...

LARS &	operator= (const LARS &other)
	Copy the given LARS object. More...

LARS &	operator= (LARS &&other)
	Take ownership of the given LARS object. More...

void	Predict (const arma::mat &points, arma::rowvec &predictions, const bool rowMajor=false) const
	Predict y_i for each data point in the given data matrix using the currently-trained LARS model. More...

template < typename Archive >
void	serialize (Archive &ar, const uint32_t)
	Serialize the LARS model. More...

double	Tolerance () const
	Get the tolerance for maximum correlation during training. More...

double &	Tolerance ()
	Modify the tolerance for maximum correlation during training. More...

double	Train (const arma::mat &data, const arma::rowvec &responses, arma::vec &beta, const bool transposeData=true)
	Run LARS. More...

double	Train (const arma::mat &data, const arma::rowvec &responses, const bool transposeData=true)
	Run LARS. More...

bool	UseCholesky () const
	Get whether to use the Cholesky decomposition. More...

bool &	UseCholesky ()
	Modify whether to use the Cholesky decomposition. More...

Detailed Description

An implementation of LARS, a stage-wise homotopy-based algorithm for l1-regularized linear regression (LASSO) and l1+l2 regularized linear regression (Elastic Net).

Let 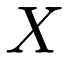$ X $ be a matrix where each row is a point and each column is a dimension and let 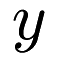$ y $ be a vector of responses.

The Elastic Net problem is to solve

$\min_{\beta} 0.5 || X \beta - y ||_2^2 + \lambda_1 || \beta ||_1 + 0.5 \lambda_2 || \beta ||_2^2$

where $\beta$ is the vector of regression coefficients.

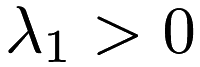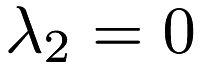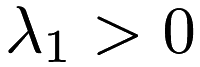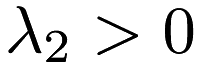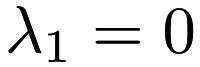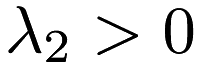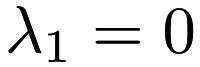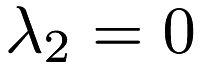If $\lambda_1 > 0$ and $\lambda_2 = 0$ , the problem is the LASSO. If $\lambda_1 > 0$ and $\lambda_2 > 0$ , the problem is the elastic net. If $\lambda_1 = 0$ and $\lambda_2 > 0$ , the problem is ridge regression. If $\lambda_1 = 0$ and $\lambda_2 = 0$ , the problem is unregularized linear regression.

Note: This algorithm is not recommended for use (in terms of efficiency) when 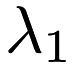$\lambda_1$ = 0.

For more details, see the following papers:

@article{efron2004least,
  title={Least angle regression},
  author={Efron, B. and Hastie, T. and Johnstone, I. and Tibshirani, R.},
  journal={The Annals of statistics},
  volume={32},
  number={2},
  pages={407--499},
  year={2004},
  publisher={Institute of Mathematical Statistics}
}

@article{zou2005regularization,
  title={Regularization and variable selection via the elastic net},
  author={Zou, H. and Hastie, T.},
  journal={Journal of the Royal Statistical Society Series B},
  volume={67},
  number={2},
  pages={301--320},
  year={2005},
  publisher={Royal Statistical Society}
}

Definition at line 89 of file lars.hpp.

Constructor & Destructor Documentation

◆ LARS() [1/6]

LARS	(	const bool	useCholesky = `false`,
		const double	lambda1 = `0.0`,
		const double	lambda2 = `0.0`,
		const double	tolerance = `1e-16`
	)

Set the parameters to LARS.

Both lambda1 and lambda2 default to 0.

Parameters

useCholesky	Whether or not to use Cholesky decomposition when solving linear system (as opposed to using the full Gram matrix).
lambda1	Regularization parameter for l1-norm penalty.
lambda2	Regularization parameter for l2-norm penalty.
tolerance	Run until the maximum correlation of elements in (X^T y) is less than this.

◆ LARS() [2/6]

LARS	(	const bool	useCholesky,
		const arma::mat &	gramMatrix,
		const double	lambda1 = `0.0`,
		const double	lambda2 = `0.0`,
		const double	tolerance = `1e-16`
	)

Set the parameters to LARS, and pass in a precalculated Gram matrix.

Both lambda1 and lambda2 default to 0.

Parameters

useCholesky	Whether or not to use Cholesky decomposition when solving linear system (as opposed to using the full Gram matrix).
gramMatrix	Gram matrix.
lambda1	Regularization parameter for l1-norm penalty.
lambda2	Regularization parameter for l2-norm penalty.
tolerance	Run until the maximum correlation of elements in (X^T y) is less than this.

◆ LARS() [3/6]

LARS	(	const arma::mat &	data,
		const arma::rowvec &	responses,
		const bool	transposeData = `true`,
		const bool	useCholesky = `false`,
		const double	lambda1 = `0.0`,
		const double	lambda2 = `0.0`,
		const double	tolerance = `1e-16`
	)

Set the parameters to LARS and run training.

Both lambda1 and lambda2 are set by default to 0.

Parameters

data	Input data.
responses	A vector of targets.
transposeData	Should be true if the input data is column-major and false otherwise.
useCholesky	Whether or not to use Cholesky decomposition when solving linear system (as opposed to using the full Gram matrix).
lambda1	Regularization parameter for l1-norm penalty.
lambda2	Regularization parameter for l2-norm penalty.
tolerance	Run until the maximum correlation of elements in (X^T y) is less than this.

◆ LARS() [4/6]

LARS	(	const arma::mat &	data,
		const arma::rowvec &	responses,
		const bool	transposeData,
		const bool	useCholesky,
		const arma::mat &	gramMatrix,
		const double	lambda1 = `0.0`,
		const double	lambda2 = `0.0`,
		const double	tolerance = `1e-16`
	)

Set the parameters to LARS, pass in a precalculated Gram matrix, and run training.

Both lambda1 and lambda2 are set by default to 0.

Parameters

data	Input data.
responses	A vector of targets.
transposeData	Should be true if the input data is column-major and false otherwise.
useCholesky	Whether or not to use Cholesky decomposition when solving linear system (as opposed to using the full Gram matrix).
gramMatrix	Gram matrix.
lambda1	Regularization parameter for l1-norm penalty.
lambda2	Regularization parameter for l2-norm penalty.
tolerance	Run until the maximum correlation of elements in (X^T y) is less than this.

◆ LARS() [5/6]

LARS ( const LARS & other )

Construct the LARS object by copying the given LARS object.

Parameters

other LARS object to copy.

◆ LARS() [6/6]

LARS ( LARS && other )

Construct the LARS object by taking ownership of the given LARS object.

Parameters

other LARS object to take ownership of.

Member Function Documentation

◆ ActiveSet()

const std::vector<size_t>& ActiveSet ( ) const

inline

Access the set of active dimensions.

Definition at line 273 of file lars.hpp.

◆ Beta()

const arma::vec& Beta ( ) const

inline

Access the solution coefficients.

Definition at line 280 of file lars.hpp.

◆ BetaPath()

const std::vector<arma::vec>& BetaPath ( ) const

inline

Access the set of coefficients after each iteration; the solution is the last element.

Definition at line 277 of file lars.hpp.

◆ ComputeError()

double ComputeError	(	const arma::mat &	matX,
		const arma::rowvec &	y,
		const bool	rowMajor = `false`
	)

Compute cost error of the given data matrix using the currently-trained LARS model.

Only ||y-beta*X||2 is used to calculate cost error.

Parameters

matX	Column-major input data (or row-major input data if rowMajor = true).
y	responses A vector of targets.
rowMajor	Should be true if the data points matrix is row-major and false otherwise.

Returns: The minimum cost error.

Referenced by LARS::MatUtriCholFactor().

◆ Lambda1() [1/2]

double Lambda1 ( ) const

inline

Get the L1 regularization coefficient.

Definition at line 253 of file lars.hpp.

◆ Lambda1() [2/2]

double& Lambda1 ( )

inline

Modify the L1 regularization coefficient.

Definition at line 255 of file lars.hpp.

◆ Lambda2() [1/2]

double Lambda2 ( ) const

inline

Get the L2 regularization coefficient.

Definition at line 258 of file lars.hpp.

◆ Lambda2() [2/2]

double& Lambda2 ( )

inline

Modify the L2 regularization coefficient.

Definition at line 260 of file lars.hpp.

◆ LambdaPath()

const std::vector<double>& LambdaPath ( ) const

inline

Access the set of values for lambda1 after each iteration; the solution is the last element.

Definition at line 284 of file lars.hpp.

◆ MatUtriCholFactor()

const arma::mat& MatUtriCholFactor ( ) const

inline

Access the upper triangular cholesky factor.

Definition at line 287 of file lars.hpp.

References LARS::ComputeError(), and LARS::serialize().

◆ operator=() [1/2]

LARS& operator= ( const LARS & other )

Copy the given LARS object.

Parameters

other LARS object to copy.

◆ operator=() [2/2]

LARS& operator= ( LARS && other )

Take ownership of the given LARS object.

Parameters

other LARS object to take ownership of.

◆ Predict()

void Predict	(	const arma::mat &	points,
		arma::rowvec &	predictions,
		const bool	rowMajor = `false`
	)		const

Predict y_i for each data point in the given data matrix using the currently-trained LARS model.

Parameters

points	The data points to regress on.
predictions	y, which will contained calculated values on completion.
rowMajor	Should be true if the data points matrix is row-major and false otherwise.

◆ serialize()

void serialize	(	Archive &	ar,
		const uint32_t
	)

Serialize the LARS model.

Referenced by LARS::MatUtriCholFactor().

◆ Tolerance() [1/2]

double Tolerance ( ) const

inline

Get the tolerance for maximum correlation during training.

Definition at line 268 of file lars.hpp.

◆ Tolerance() [2/2]

double& Tolerance ( )

inline

Modify the tolerance for maximum correlation during training.

Definition at line 270 of file lars.hpp.

◆ Train() [1/2]

double Train	(	const arma::mat &	data,
		const arma::rowvec &	responses,
		arma::vec &	beta,
		const bool	transposeData = `true`
	)

Run LARS.

The input matrix (like all mlpack matrices) should be column-major – each column is an observation and each row is a dimension. However, because LARS is more efficient on a row-major matrix, this method will (internally) transpose the matrix. If this transposition is not necessary (i.e., you want to pass in a row-major matrix), pass 'false' for the transposeData parameter.

Parameters

data	Column-major input data (or row-major input data if rowMajor = true).
responses	A vector of targets.
beta	Vector to store the solution (the coefficients) in.
transposeData	Set to false if the data is row-major.

Returns: minimum cost error(||y-beta*X||2 is used to calculate error).

◆ Train() [2/2]

double Train	(	const arma::mat &	data,
		const arma::rowvec &	responses,
		const bool	transposeData = `true`
	)

Run LARS.

The input matrix (like all mlpack matrices) should be column-major – each column is an observation and each row is a dimension. However, because LARS is more efficient on a row-major matrix, this method will (internally) transpose the matrix. If this transposition is not necessary (i.e., you want to pass in a row-major matrix), pass 'false' for the transposeData parameter.

Parameters

data	Input data.
responses	A vector of targets.
transposeData	Should be true if the input data is column-major and false otherwise.

Returns: minimum cost error(||y-beta*X||2 is used to calculate error).

◆ UseCholesky() [1/2]

bool UseCholesky ( ) const

inline

Get whether to use the Cholesky decomposition.

Definition at line 263 of file lars.hpp.

◆ UseCholesky() [2/2]

bool& UseCholesky ( )

inline

Modify whether to use the Cholesky decomposition.

Definition at line 265 of file lars.hpp.

The documentation for this class was generated from the following file:

/home/ryan/src/mlpack.org/_src/mlpack-git/src/mlpack/methods/lars/lars.hpp

Public Member Functions

Detailed Description

Constructor & Destructor Documentation

◆ LARS() [1/6]

◆ LARS() [2/6]

◆ LARS() [3/6]

◆ LARS() [4/6]

◆ LARS() [5/6]

◆ LARS() [6/6]

Member Function Documentation

◆ ActiveSet()

◆ Beta()

◆ BetaPath()

◆ ComputeError()

◆ Lambda1() [1/2]

◆ Lambda1() [2/2]

◆ Lambda2() [1/2]

◆ Lambda2() [2/2]

◆ LambdaPath()

◆ MatUtriCholFactor()

◆ operator=() [1/2]

◆ operator=() [2/2]

◆ Predict()

◆ serialize()

◆ Tolerance() [1/2]

◆ Tolerance() [2/2]

◆ Train() [1/2]

◆ Train() [2/2]

◆ UseCholesky() [1/2]

◆ UseCholesky() [2/2]