Introduction

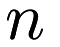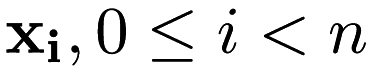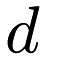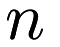Linear regression and ridge regression are simple machine learning techniques that aim to estimate the parameters of a linear model. Assuming we have $n$ predictor points $\mathbf{x_i}, 0 \le i < n$ of dimensionality $d$ and $n$ responses 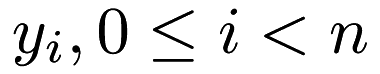$y_i, 0 \le i < n$ , we are trying to estimate the best fit for 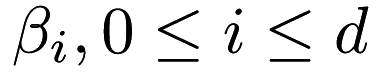$\beta_i, 0 \le i \le d$ in the linear model

$y_i = \beta_0 + \displaystyle\sum_{j = 1}^{d} \beta_j x_{ij}$

for each predictor 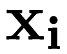$\mathbf{x_i}$ and response 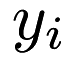$y_i$ . If we take each predictor 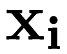$\mathbf{x_i}$ as a row in the matrix 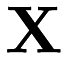$\mathbf{X}$ and each response 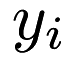$y_i$ as an entry of the vector 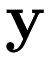$\mathbf{y}$ , we can represent the model in vector form:

$\mathbf{y} = \mathbf{X} \mathbf{\beta} + \beta_0$

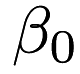The result of this method is the vector $\mathbf{\beta}$ , including the offset term (or intercept term) $\beta_0$ .

mlpack provides:

a simple command-line executable to perform linear regression or ridge regression
a simple C++ interface to perform linear regression or ridge regression

Command-Line 'mlpack_linear_regression'

The simplest way to perform linear regression or ridge regression in mlpack is to use the mlpack_linear_regression executable. This program will perform linear regression and place the resultant coefficients into one file.

The output file holds a vector of coefficients in increasing order of dimension; that is, the offset term ( 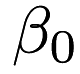$\beta_0$ ), the coefficient for dimension 1 ( 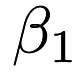$\beta_1$ , then dimension 2 ( 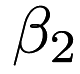$\beta_2$ ) and so forth, as well as the intercept. This executable can also predict the 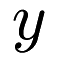$y$ values of a second dataset based on the computed coefficients.

Below are several examples of simple usage (and the resultant output). The option is used so that verbose output is given. Further documentation on each individual option can be found by typing

$ mlpack_linear_regression --help

One file, generating the function coefficients

$ mlpack_linear_regression --training_file dataset.csv -v -M lr.xml
[INFO ] Loading 'dataset.csv' as CSV data.  Size is 2 x 5.
[INFO ]
[INFO ] Execution parameters:
[INFO ]   help: false
[INFO ]   info: ""
[INFO ]   input_model_file: ""
[INFO ]   lambda: 0
[INFO ]   output_model_file: lr.xml
[INFO ]   output_predictions: predictions.csv
[INFO ]   test_file: ""
[INFO ]   training_file: dataset.csv
[INFO ]   training_responses: ""
[INFO ]   verbose: true
[INFO ]   version: false
[INFO ]
[INFO ] Program timers:
[INFO ]   load_regressors: 0.000263s
[INFO ]   loading_data: 0.000220s
[INFO ]   regression: 0.000392s
[INFO ]   total_time: 0.001920s

Convenient program timers are given for different parts of the calculation at the bottom of the output, as well as the parameters the simulation was run with. Now, if we look at the output model file, which is lr.xml,

$ cat dataset.csv
0,0
1,1
2,2
3,3
4,4
$ cat lr.xml
<?xml version="1.0" encoding="utf-8"?>
<cereal>
  <model>
    <cereal_class_version>0</cereal_class_version>
    <parameters>
      <n_rows>2</n_rows>
      <n_cols>1</n_cols>
      <vec_state>1</vec_state>
      <elem>0</elem>
      <elem>1</elem>
    </parameters>
    <lambda>0</lambda>
    <intercept>true</intercept>
  </model>
</cereal>

As you can see, the function for this input is 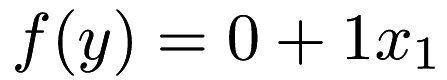$f(y)=0+1x_1$ . We can see that the model we have trained catches this; in the <parameters> section of lr.xml, we can see that there are two elements, which are (approximately) 0 and 1. The first element corresponds to the intercept 0, and the second column corresponds to the coefficient 1 for the variable 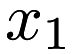$x_1$ . Note that in this example, the regressors for the dataset are the second column. That is, the dataset is one dimensional, and the last column has the 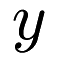$y$ values, or responses, for each row. You can specify these responses in a separate file if you want, using the –input_responses, or -r, option.

Train a multivariate linear regression model

Multivariate linear regression means that the response variable is predicted by more than just one input variable. In this example we will try to fit a multivariate linear regression model to data that contains four variables, stored in dataset_2.csv.

$ cat dataset_2.csv
0,0,0,0,14
1,1,1,1,24
2,1,0,2,27
1,2,2,2,32
-1,-3,0,2,17

Now let's run mlpack_linear_regression as usual:

$ mlpack_linear_regression --training_file dataset_2.csv -v -M lr.xml
[INFO ] Loading 'dataset_2.csv' as CSV data.  Size is 5 x 5.
[INFO ] 
[INFO ] Execution parameters:
[INFO ]   help: 0
[INFO ]   info: 
[INFO ]   input_model_file: 
[INFO ]   lambda: 0
[INFO ]   output_model_file: lr.xml
[INFO ]   output_predictions_file: 
[INFO ]   test_file: 
[INFO ]   training_file: dataset_2.csv
[INFO ]   training_responses_file: 
[INFO ]   verbose: 1
[INFO ]   version: 0
[INFO ] Program timers:
[INFO ]   load_regressors: 0.000060s
[INFO ]   loading_data: 0.000050s
[INFO ]   regression: 0.000049s
[INFO ]   total_time: 0.000118s
$ cat lr.xml 
<?xml version="1.0" encoding="utf-8"?>
<cereal>
  <model>
    <cereal_class_version>0</cereal_class_version>
    <parameters>
      <n_rows>5</n_rows>
      <n_cols>1</n_cols>
      <vec_state>1</vec_state>
      <elem>14.00000000000002</elem>
      <elem>1.9999999999999447</elem>
      <elem>1.0000000000000431</elem>
      <elem>2.9999999999999516</elem>
      <elem>4.0000000000000249</elem>
    </parameters>
    <lambda>0</lambda>
    <intercept>true</intercept>
  </model>
</cereal>

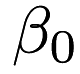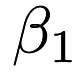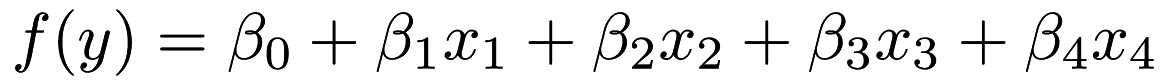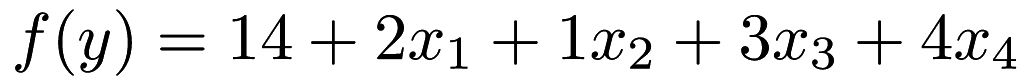If we take a look at the lr.xml output we can see the <parameters> part has five elements which the first corresponds to $\beta_0$ , the second corresponds to $\beta_1$ , and so on. This is equivalent to $f(y) = \beta_0 + \beta_1x_1 + \beta_2x_2 + \beta_3x_3 + \beta_4x_4$ or $f(y)=14+2x_1+1x_2+3x_3+4x_4$ .

Compute model and predict at the same time

$ mlpack_linear_regression --training_file dataset.csv --test_file predict.csv --output_predictions_file predictions.csv \
> -v
[WARN ] '--output_predictions_file (-o)' ignored because '--test_file (-T)' is specified!
[INFO ] Loading 'dataset.csv' as CSV data.  Size is 2 x 5.
[INFO ] Loading 'predict.csv' as raw ASCII formatted data.  Size is 1 x 3.
[INFO ] Saving CSV data to 'predictions.csv'.
[INFO ] 
[INFO ] Execution parameters:
[INFO ]   help: 0
[INFO ]   info: 
[INFO ]   input_model_file: 
[INFO ]   lambda: 0
[INFO ]   output_model_file: 
[INFO ]   output_predictions_file: 'predictions.csv' (1x3 matrix)
[INFO ]   test_file: 'predict.csv' (0x0 matrix)
[INFO ]   training_file: 'dataset.csv' (0x0 matrix)
[INFO ]   training_responses_file: ''
[INFO ]   verbose: 1
[INFO ]   version: 0
[INFO ] Program timers:
[INFO ]   load_regressors: 0.000069s
[INFO ]   load_test_points: 0.000031s
[INFO ]   loading_data: 0.000079s
[INFO ]   prediction: 0.000001s
[INFO ]   regression: 0.000054s
[INFO ]   saving_data: 0.000055s
[INFO ]   total_time: 0.000203s
$ cat dataset.csv
0,0
1,1
2,2
3,3
4,4
$ cat predict.csv
2
3
4
$ cat predictions.csv
2.0000000000e+00
3.0000000000e+00
4.0000000000e+00

We used the same dataset, so we got the same parameters. The key thing to note about the predict.csv dataset is that it has the same dimensionality as the dataset used to create the model, one. If the model generating dataset has 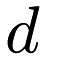$d$ dimensions, so must the dataset we want to predict for.

Prediction using a precomputed model

$ mlpack_linear_regression --input_model_file lr.xml --test_file predict.csv --output_predictions_file predictions.csv -v
[WARN ] '--output_predictions_file (-o)' ignored because '--test_file (-T)' is specified!
[INFO ] Loading 'predict.csv' as raw ASCII formatted data.  Size is 1 x 3.
[INFO ] Saving CSV data to 'predictions.csv'.
[INFO ] 
[INFO ] Execution parameters:
[INFO ]   help: 0
[INFO ]   info: 
[INFO ]   input_model_file: lr.xml
[INFO ]   lambda: 0
[INFO ]   output_model_file: 
[INFO ]   output_predictions_file: 'predictions.csv' (1x3 matrix)
[INFO ]   test_file: 'predict.csv' (0x0 matrix)
[INFO ]   training_file: ''
[INFO ]   training_responses_file: ''
[INFO ]   verbose: 1
[INFO ]   version: 0
[INFO ] Program timers:
[INFO ]   load_model: 0.000051s
[INFO ]   load_test_points: 0.000052s
[INFO ]   loading_data: 0.000044s
[INFO ]   prediction: 0.000010s
[INFO ]   saving_data: 0.000079s
[INFO ]   total_time: 0.000160s
$ cat lr.xml
<?xml version="1.0" encoding="utf-8"?>
<cereal>
  <model>
    <cereal_class_version>0</cereal_class_version>
    <parameters>
      <n_rows>2</n_rows>
      <n_cols>1</n_cols>
      <vec_state>1</vec_state>
      <elem>0</elem>
      <elem>1</elem>
    </parameters>
    <lambda>0</lambda>
    <intercept>true</intercept>
  </model>
</cereal>
$ cat predict.csv
2
3
4
$ cat predictions.csv
2.0000000000e+00
3.0000000000e+00
4.0000000000e+00

Using ridge regression

Sometimes, the input matrix of predictors has a covariance matrix that is not invertible, or the system is overdetermined. In this case, ridge regression is useful: it adds a normalization term to the covariance matrix to make it invertible. Ridge regression is a standard technique and documentation for the mathematics behind it can be found anywhere on the Internet. In short, the covariance matrix

$\mathbf{X}' \mathbf{X}$

is replaced with

$\mathbf{X}' \mathbf{X} + \lambda \mathbf{I}$

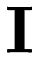where $\mathbf{I}$ is the identity matrix. So, a 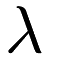$\lambda$ parameter greater than zero should be specified to perform ridge regression, using the –lambda (or -l) option. An example is given below.

$ mlpack_linear_regression --training_file dataset.csv -v --lambda 0.5 -M lr.xml
[INFO ] Loading 'dataset.csv' as CSV data.  Size is 2 x 5.
[INFO ]
[INFO ] Execution parameters:
[INFO ]   help: false
[INFO ]   info: ""
[INFO ]   input_model_file: ""
[INFO ]   lambda: 0.5
[INFO ]   output_model_file: lr.xml
[INFO ]   output_predictions: predictions.csv
[INFO ]   test_file: ""
[INFO ]   training_file: dataset.csv
[INFO ]   training_responses: ""
[INFO ]   verbose: true
[INFO ]   version: false
[INFO ]
[INFO ] Program timers:
[INFO ]   load_regressors: 0.000210s
[INFO ]   loading_data: 0.000170s
[INFO ]   regression: 0.000332s
[INFO ]   total_time: 0.001835s

Further documentation on options should be found by using the –help option.

The 'LinearRegression' class

The 'LinearRegression' class is a simple implementation of linear regression.

Using the LinearRegression class is very simple. It has two available constructors; one for generating a model from a matrix of predictors and a vector of responses, and one for loading an already computed model from a given file.

The class provides one method that performs computation:

void Predict(const arma::mat& points, arma::vec& predictions);

Once you have generated or loaded a model, you can call this method and pass it a matrix of data points to predict values for using the model. The second parameter, predictions, will be modified to contain the predicted values corresponding to each row of the points matrix.

Generating a model

#include <mlpack/methods/linear_regression/linear_regression.hpp>
using namespace mlpack::regression;
arma::mat data; // The dataset itself.
arma::vec responses; // The responses, one row for each row in data.
// Regress.
LinearRegression lr(data, responses);
// Get the parameters, or coefficients.
arma::vec parameters = lr.Parameters();

Setting a model

Assuming you already have a model and do not need to create one, this is how you would set the parameters for a LinearRegression instance.

arma::vec parameters; // Your model.
LinearRegression lr; // Create a new LinearRegression instance or reuse one.
lr.Parameters() = parameters; // Set the model.

Load a model from a file

If you have a generated model in a file somewhere you would like to load and use, you can use data::Load() to load it.

std::string filename; // The path and name of your file.
LinearRegression lr;
data::Load(filename, "lr_model", lr);

Prediction

Once you have generated or loaded a model using one of the aforementioned methods, you can predict values for a dataset.

LinearRegression lr();
// Load or generate your model.
// The dataset we want to predict on; each row is a data point.
arma::mat points;
// This will store the predictions; one row for each point.
arma::vec predictions;
lr.Predict(points, predictions); // Predict.
// Now, the vector 'predictions' will contain the predicted values.

Setting lambda for ridge regression

As discussed in Prediction using a precomputed model, ridge regression is useful when the covariance of the predictors is not invertible. The standard constructor can be used to set a value of lambda:

#include <mlpack/methods/linear_regression/linear_regression.hpp>
using namespace mlpack::regression;
arma::mat data; // The dataset itself.
arma::vec responses; // The responses, one row for each row in data.
// Regress, with a lambda of 0.5.
LinearRegression lr(data, responses, 0.5);
// Get the parameters, or coefficients.
arma::vec parameters = lr.Parameters();

In addition, the Lambda() function can be used to get or modify the lambda value:

LinearRegression lr;
lr.Lambda() = 0.5;
Log::Info << "Lambda is " << lr.Lambda() << "." << std::endl;

Further documentation

For further documentation on the LinearRegression class, consult the complete API documentation.