The MSE (Mean squared error) gain, is a measure of set purity based on the variance of response values present in the node. More...

Public Member Functions
std::tuple< double, double >	BinaryGains ()
	Calculates the mean squared error gain for the left and right children for the current index. More...

template<bool UseWeights, typename ResponsesType , typename WeightVecType >
void	BinaryScanInitialize (const ResponsesType &responses, const WeightVecType &weights, const size_t minimum)
	Caches the prefix sum of squares to efficiently compute gain value for each split. More...

template<bool UseWeights, typename ResponsesType , typename WeightVecType >
void	BinaryStep (const ResponsesType &responses, const WeightVecType &weights, const size_t index)
	Updates the statistics for the given index. More...

template<bool UseWeights, typename ResponsesType , typename WeightsType >
double	OutputLeafValue (const ResponsesType &responses, const WeightsType &weights)
	Returns the output value for each leaf node for prediction. More...

Static Public Member Functions
template<bool UseWeights, typename VecType , typename WeightVecType >
static double	Evaluate (const VecType &values, const WeightVecType &weights, const size_t begin, const size_t end)
	Evaluate the mean squared error gain of values from begin to end index. More...

template<bool UseWeights, typename VecType , typename WeightVecType >
static double	Evaluate (const VecType &values, const WeightVecType &weights)
	Evaluate the MSE gain on the complete vector. More...

Detailed Description

The MSE (Mean squared error) gain, is a measure of set purity based on the variance of response values present in the node.

This is same thing as negation of variance of dependent variable in the node as we will try to maximize this quantity to maximize gain (and thus reduce variance of a set).

Definition at line 28 of file mse_gain.hpp.

Member Function Documentation

◆ BinaryGains()

std::tuple<double, double> BinaryGains ( )

inline

Calculates the mean squared error gain for the left and right children for the current index.

X = array of values of size n.

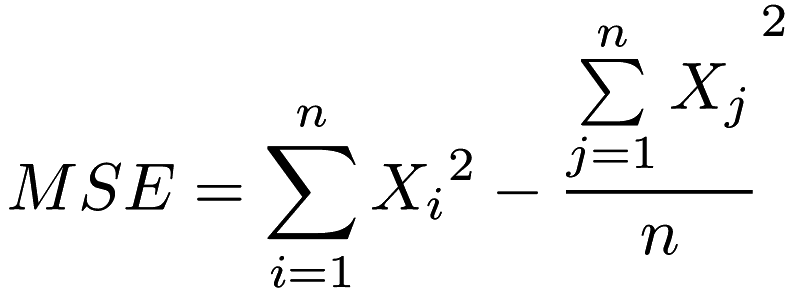
$\begin{eqnarray*} MSE = \sum\limits_{i=1}^n {X_i}^2 - {\dfrac{\sum\limits_{j=1}^n X_j}{n}}^2 \end{eqnarray*}$

Definition at line 133 of file mse_gain.hpp.

◆ BinaryScanInitialize()

void BinaryScanInitialize	(	const ResponsesType &	responses,
		const WeightVecType &	weights,
		const size_t	minimum
	)

inline

Caches the prefix sum of squares to efficiently compute gain value for each split.

It also computes the initial mean for left and right child.

Parameters

responses	The set of responses on which statistics are computed.
weights	The set of weights associated to each response.
minimum	The minimum number of elements in a leaf.

Definition at line 151 of file mse_gain.hpp.

◆ BinaryStep()

void BinaryStep	(	const ResponsesType &	responses,
		const WeightVecType &	weights,
		const size_t	index
	)

inline

Updates the statistics for the given index.

Parameters

responses	The set of responses on which statistics are computed.
weights	The set of weights associated to each response.
index	The current index.

Definition at line 230 of file mse_gain.hpp.

◆ Evaluate() [1/2]

static double Evaluate	(	const VecType &	values,
		const WeightVecType &	weights,
		const size_t	begin,
		const size_t	end
	)

inlinestatic

Evaluate the mean squared error gain of values from begin to end index.

Note that gain can be slightly greater than 0 due to floating-point representation issues. Thus if you are checking for perfect fit, be sure to use 'gain >= 0.0' and not 'gain == 0.0'. The values vector should always be of type arma::Row<double> or arma::rowvec.

Parameters

values	Set of values to evaluate MAD gain on.
weights	Weights associated to each value.
begin	Start index.
end	End index.

Definition at line 44 of file mse_gain.hpp.

References Sum(), and WeightedSum().

◆ Evaluate() [2/2]

static double Evaluate	(	const VecType &	values,
		const WeightVecType &	weights
	)

inlinestatic

Evaluate the MSE gain on the complete vector.

Parameters

values	Set of values to evaluate MSE gain on.
weights	Weights associated to each value.

Definition at line 88 of file mse_gain.hpp.

◆ OutputLeafValue()

double OutputLeafValue	(	const ResponsesType &	responses,
		const WeightsType &	weights
	)

inline

Returns the output value for each leaf node for prediction.

The output value is calculated as the average of all the points in that leaf node. This calculation is specific to regression trees only.

Definition at line 104 of file mse_gain.hpp.

References Sum(), and WeightedSum().

The documentation for this class was generated from the following file:

/home/ryan/src/mlpack.org/_src/mlpack-git/src/mlpack/methods/decision_tree/mse_gain.hpp

Public Member Functions

Static Public Member Functions

Detailed Description

Member Function Documentation

◆ BinaryGains()

◆ BinaryScanInitialize()

◆ BinaryStep()

◆ Evaluate() [1/2]

◆ Evaluate() [2/2]

◆ OutputLeafValue()