A Bayesian approach to the maximum likelihood estimation of the parameters 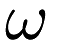 of the linear regression model.
More...
of the linear regression model.
More...
Public Member Functions | |
| BayesianLinearRegression (const bool centerData=true, const bool scaleData=false, const size_t maxIterations=50, const double tolerance=1e-4) | |
| Set the parameters of Bayesian Ridge regression object. More... | |
| double | Alpha () const |
| Get the precision (or inverse variance) of the gaussian prior. More... | |
| double | Beta () const |
| Get the precision (or inverse variance) beta of the model. More... | |
| bool | CenterData () const |
| Get whether the data will be centered during training. More... | |
| bool & | CenterData () |
| Modify whether the data will be centered during training. More... | |
| const arma::colvec & | DataOffset () const |
| Get the mean vector computed on the features over the training points. More... | |
| const arma::colvec & | DataScale () const |
| Get the vector of standard deviations computed on the features over the training points. More... | |
| size_t | MaxIterations () const |
| Get the maximum number of iterations for training. More... | |
| size_t & | MaxIterations () |
| Modify the maximum number of iterations for training. More... | |
| const arma::colvec & | Omega () const |
| Get the solution vector. More... | |
| void | Predict (const arma::mat &points, arma::rowvec &predictions) const |
Predict 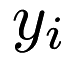 for each data point in the given data matrix using the currently-trained Bayesian Ridge model. More... for each data point in the given data matrix using the currently-trained Bayesian Ridge model. More... | |
| void | Predict (const arma::mat &points, arma::rowvec &predictions, arma::rowvec &std) const |
Predict 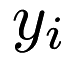 and the standard deviation of the predictive posterior distribution for each data point in the given data matrix, using the currently-trained Bayesian Ridge estimator. More... and the standard deviation of the predictive posterior distribution for each data point in the given data matrix, using the currently-trained Bayesian Ridge estimator. More... | |
| double | ResponsesOffset () const |
| Get the mean value of the train responses. More... | |
| double | RMSE (const arma::mat &data, const arma::rowvec &responses) const |
| Compute the Root Mean Square Error between the predictions returned by the model and the true responses. More... | |
| bool | ScaleData () const |
| Get whether the data will be scaled by standard deviations during training. More... | |
| bool & | ScaleData () |
| Modify whether the data will be scaled by standard deviations during training. More... | |
template < typename Archive > | |
| void | serialize (Archive &ar, const uint32_t version) |
| Serialize the BayesianLinearRegression model. More... | |
| double | Tolerance () const |
| Get the tolerance for training to converge. More... | |
| double & | Tolerance () |
| Modify the tolerance for training to converge. More... | |
| double | Train (const arma::mat &data, const arma::rowvec &responses) |
| Run BayesianLinearRegression. More... | |
| double | Variance () const |
| Get the estimated variance. More... | |
Detailed Description
A Bayesian approach to the maximum likelihood estimation of the parameters 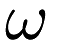 of the linear regression model.
of the linear regression model.
The Complexity is governed by the addition of a gaussian isotropic prior of precision 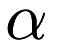 over
over 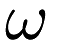 :
:
![\[ p(\omega|\alpha) = \mathcal{N}(\omega|0, \alpha^{-1}I) \]](form_143.png)
The optimization procedure calculates the posterior distribution of 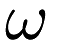 knowing the data by maximizing an approximation of the log marginal likelihood derived from a type II maximum likelihood approximation. The determination of
knowing the data by maximizing an approximation of the log marginal likelihood derived from a type II maximum likelihood approximation. The determination of 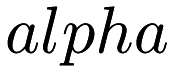 and of the noise precision
and of the noise precision 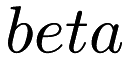 is part of the optimization process, leading to an automatic determination of w. The model being entirely based on probabilty distributions, uncertainties are available and easly computed for both the parameters and the predictions.
is part of the optimization process, leading to an automatic determination of w. The model being entirely based on probabilty distributions, uncertainties are available and easly computed for both the parameters and the predictions.
The advantage over linear regression and ridge regression is that the regularization is determined from all the training data alone without any require to an hold out method.
The code below is an implementation of the maximization of the evidence function described in the section 3.5.2 of the C.Bishop book, Pattern Recognition and Machine Learning.
Example of use:
Definition at line 99 of file bayesian_linear_regression.hpp.
Constructor & Destructor Documentation
◆ BayesianLinearRegression()
| BayesianLinearRegression | ( | const bool | centerData = true, |
| const bool | scaleData = false, |
||
| const size_t | maxIterations = 50, |
||
| const double | tolerance = 1e-4 |
||
| ) |
Set the parameters of Bayesian Ridge regression object.
The regularization parameter is automatically set to its optimal value by maximization of the marginal likelihood.
- Parameters
-
centerData Whether or not center the data according to the examples. scaleData Whether or not scale the data according to the standard deviation of each feature. maxIterations Maximum number of iterations for convergency. tolerance Level from which the solution is considered sufficientlly stable.
Member Function Documentation
◆ Alpha()
|
inline |
Get the precision (or inverse variance) of the gaussian prior.
Train() must be called before.
- Returns
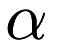
Definition at line 181 of file bayesian_linear_regression.hpp.
◆ Beta()
|
inline |
Get the precision (or inverse variance) beta of the model.
Train() must be called before.
- Returns

Definition at line 189 of file bayesian_linear_regression.hpp.
Referenced by BayesianLinearRegression::Variance().
◆ CenterData() [1/2]
|
inline |
Get whether the data will be centered during training.
Definition at line 221 of file bayesian_linear_regression.hpp.
◆ CenterData() [2/2]
|
inline |
Modify whether the data will be centered during training.
Definition at line 223 of file bayesian_linear_regression.hpp.
◆ DataOffset()
|
inline |
Get the mean vector computed on the features over the training points.
- Returns
- responsesOffset
Definition at line 203 of file bayesian_linear_regression.hpp.
◆ DataScale()
|
inline |
Get the vector of standard deviations computed on the features over the training points.
- Returns
- dataOffset
Definition at line 211 of file bayesian_linear_regression.hpp.
◆ MaxIterations() [1/2]
|
inline |
Get the maximum number of iterations for training.
Definition at line 233 of file bayesian_linear_regression.hpp.
◆ MaxIterations() [2/2]
|
inline |
Modify the maximum number of iterations for training.
Definition at line 235 of file bayesian_linear_regression.hpp.
◆ Omega()
|
inline |
Get the solution vector.
- Returns
- omega Solution vector.
Definition at line 173 of file bayesian_linear_regression.hpp.
◆ Predict() [1/2]
| void Predict | ( | const arma::mat & | points, |
| arma::rowvec & | predictions | ||
| ) | const |
Predict 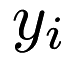 for each data point in the given data matrix using the currently-trained Bayesian Ridge model.
for each data point in the given data matrix using the currently-trained Bayesian Ridge model.
- Parameters
-
points The data points to apply the model. predictions y, Contains the predicted values on completion.
- Returns
- Root mean squared error computed on the train set.
◆ Predict() [2/2]
| void Predict | ( | const arma::mat & | points, |
| arma::rowvec & | predictions, | ||
| arma::rowvec & | std | ||
| ) | const |
Predict 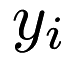 and the standard deviation of the predictive posterior distribution for each data point in the given data matrix, using the currently-trained Bayesian Ridge estimator.
and the standard deviation of the predictive posterior distribution for each data point in the given data matrix, using the currently-trained Bayesian Ridge estimator.
- Parameters
-
points The data point to apply the model. predictions Vector which will contain calculated values on completion. std Standard deviations of the predictions.
◆ ResponsesOffset()
|
inline |
Get the mean value of the train responses.
- Returns
- responsesOffset
Definition at line 218 of file bayesian_linear_regression.hpp.
◆ RMSE()
| double RMSE | ( | const arma::mat & | data, |
| const arma::rowvec & | responses | ||
| ) | const |
Compute the Root Mean Square Error between the predictions returned by the model and the true responses.
- Parameters
-
data Data points to predict responses A vector of targets.
- Returns
- Root mean squared error.
◆ ScaleData() [1/2]
|
inline |
Get whether the data will be scaled by standard deviations during training.
Definition at line 227 of file bayesian_linear_regression.hpp.
◆ ScaleData() [2/2]
|
inline |
Modify whether the data will be scaled by standard deviations during training.
Definition at line 230 of file bayesian_linear_regression.hpp.
◆ serialize()
| void serialize | ( | Archive & | ar, |
| const uint32_t | version | ||
| ) |
Serialize the BayesianLinearRegression model.
Referenced by BayesianLinearRegression::Tolerance().
◆ Tolerance() [1/2]
|
inline |
Get the tolerance for training to converge.
Definition at line 238 of file bayesian_linear_regression.hpp.
◆ Tolerance() [2/2]
|
inline |
Modify the tolerance for training to converge.
Definition at line 240 of file bayesian_linear_regression.hpp.
References BayesianLinearRegression::serialize().
◆ Train()
| double Train | ( | const arma::mat & | data, |
| const arma::rowvec & | responses | ||
| ) |
The input matrix (like all mlpack matrices) should be column-major – each column is an observation and each row is a dimension.
- Parameters
-
data Column-major input data, dim(P, N). responses A vector of targets, dim(N).
- Returns
- Root mean squared error.
◆ Variance()
|
inline |
Get the estimated variance.
Train() must be called before.
- Returns
- 1.0 /

Definition at line 196 of file bayesian_linear_regression.hpp.
References BayesianLinearRegression::Beta().
The documentation for this class was generated from the following file:
- /home/ryan/src/mlpack.org/_src/mlpack-git/src/mlpack/methods/bayesian_linear_regression/bayesian_linear_regression.hpp


