mlpack::kernel Namespace Reference

Kernel functions. More...

Classes
class	CauchyKernel
	The Cauchy kernel. More...
class	CosineDistance
	The cosine distance (or cosine similarity). More...
class	EpanechnikovKernel
	The Epanechnikov kernel, defined as. More...
class	ExampleKernel
	An example kernel function. More...
class	GaussianKernel
	The standard Gaussian kernel. More...
class	HyperbolicTangentKernel
	Hyperbolic tangent kernel. More...
class	KernelTraits
	This is a template class that can provide information about various kernels. More...
class	KernelTraits< CauchyKernel >
	Kernel traits for the Cauchy kernel. More...
class	KernelTraits< CosineDistance >
	Kernel traits for the cosine distance. More...
class	KernelTraits< EpanechnikovKernel >
	Kernel traits for the Epanechnikov kernel. More...
class	KernelTraits< GaussianKernel >
	Kernel traits for the Gaussian kernel. More...
class	KernelTraits< LaplacianKernel >
	Kernel traits of the Laplacian kernel. More...
class	KernelTraits< SphericalKernel >
	Kernel traits for the spherical kernel. More...
class	KernelTraits< TriangularKernel >
	Kernel traits for the triangular kernel. More...
class	KMeansSelection
	Implementation of the kmeans sampling scheme. More...
class	LaplacianKernel
	The standard Laplacian kernel. More...
class	LinearKernel
	The simple linear kernel (dot product). More...
class	NystroemMethod
class	OrderedSelection
class	PolynomialKernel
	The simple polynomial kernel. More...
class	PSpectrumStringKernel
	The p-spectrum string kernel. More...
class	RandomSelection
class	SphericalKernel
	The spherical kernel, which is 1 when the distance between the two argument points is less than or equal to the bandwidth, or 0 otherwise. More...
class	TriangularKernel
	The trivially simple triangular kernel, defined by. More...

Detailed Description

Kernel functions.

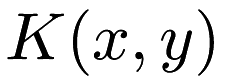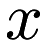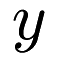This namespace contains kernel functions, which evaluate some kernel function for some arbitrary vectors and of the same dimension. The single restriction on the function 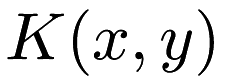is that it must satisfy Mercer's condition:

for all square integrable functions .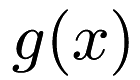

The kernels in this namespace all implement the KernelType policy. For more information, see The KernelType policy documentation.